Imagina una agencia de publicidad que recopila información sobre las interacciones del usuario para decidir qué tipo de anuncio mostrar. Eso es tan infrecuente, Google, Twitter, Facebook, y otros grandes tecnológicos que confían en los anuncios tienen perfiles personales muy buenos de sus usuarios para ayudar a entregar anuncios personalizados.
Un usuario que ha buscado recientemente teclados para juegos o tarjetas gráficas es
probablemente más probable que haga clic en anuncios sobre los mejores y más recientes videojuegos.
Puede ser difícil atender un anuncio especialmente diseñado para cada individuo, por lo que agrupar a los usuarios en categorías es una técnica común. Por ejemplo, un usuario puede ser categorizado como "Jugador" para recibir anuncios relevantes relacionados con videojuegos.
El aprendizaje automático ha sido la herramienta para llevar a cabo, como la tarea. En el nivel más fundamental, los profesionales del aprendizaje automático desean construir una herramienta que les ayude a comprender los datos. Ser capaz de etiquetar elementos de datos en categorías separadas es una excelente manera de caracterizar necesidades específicas.
El capítulo anterior se ocupó de la regresión, que trataba de ajustar una curva a los datos. Si recuerda, la curva de mejor ajuste es una función que toma como entrada un elemento de datos y le asigna un número. La creación de un modelo de aprendizaje automático en su lugar asigna etiquetas discretas a sus entradas se denomina clasificación. Es un algoritmo de aprendizaje supervisado para tratar la salida discreta. (Cada valor discreto se denomina clase). La entrada suele ser un vector de entidad, y la salida es una clase. Si solo hay dos etiquetas de clase (por ejemplo, Verdadero / Falso, Activar / Desactivar, Sí / No), llamamos a este algoritmo de aprendizaje un clasificador binario. De lo contrario, se llama un clasificador multiclase.
Hay muchos tipos de clasificadores, pero este capítulo se centrará en los que se resumen en la tabla
4.1. Cada uno tiene sus ventajas y desventajas, que profundizaremos una vez que comencemos a implementar cada uno en tensorflow.
La regresión lineal es la más fácil de implementar porque ya hemos hecho la mayor parte del trabajo duro en el último capítulo, pero como verás, es un clasificador terrible. Un clasificador mucho mejor es el algoritmo de regresión logística. Como su nombre lo indica, utilizará propiedades logarítmicas para definir una mejor función de costo. Y, por último, la regresión de softmax es un enfoque directo para resolver la clasificación multiclase. Es una generalización natural de la regresión logística. Se llama regresión softmax. porque hay una función llamada softmax que se aplica como el último paso.
Notación Formal
En notación matemática, un clasificador es una función y = f (x), donde x es el elemento de datos de entrada i "y" es la categoría de salida (figura 4.1). Adoptado de la literatura científica tradicional, a menudo nos referimos al vector de entrada "x" como la variable independiente, i "y" como la salida osea como variable dependiente.
Formalmente, una categoría con etiqueta está restringida a un rango de valores posibles. Puedes pensar en etiquetas de dos valores como variables booleanas en Python. Cuando las funciones de entrada solo tienen un conjunto fijo de valores posibles, debemos asegurarnos de que nuestro modelo pueda entender cómo manejarlos. Dado que el conjunto de funciones en un modelo generalmente trata con números reales continuos, debemos preprocesar el conjunto de datos para tener en cuenta las variables discretas, que se dividen en uno de dos tipos:
ordinales o nominales (figura 4.2).
Los valores de un tipo ordinal, como sugiere su nombre, pueden ordenarse. Por ejemplo, los valores en un conjunto de números pares del 1 al 10 son ordinales porque los enteros se pueden comparar entre sí. Por otro lado, un elemento de un conjunto de frutas (plátano, manzana, naranja) podría no tener un orden natural. Llamamos valores de un conjunto nominal, porque solo pueden ser descritos por sus nombres.
Un enfoque simple para representar variables nominales en un conjunto de datos es asignar un número a cada etiqueta. Nuestro conjunto {banana, manzana, naranja} podría ser procesado como {0, 1, 2}. Sin embargo, algunos modelos de clasificación pueden tener un fuerte sesgo acerca de cómo se comportan los datos. Por ejemplo, la regresión lineal interpretaría nuestra manzana como un punto intermedio entre un plátano y una naranja, lo que no tiene ningún sentido natural.
Una solución alternativa simple para representar categorías nominales de una variable dependiente es agregar lo que se llama variables ficticias para cada valor de la variable nominal. En este ejemplo, la variable "fruta" se eliminaría y reemplazaría por tres variables separadas: "plátano", "manzana" y "naranja". Cada variable tiene un valor de 0 o 1 (figura 4.3), dependiendo de si la categoría para esa fruta es cierta. Esto a menudo se conoce como codificación de un solo calor (one-hot encoding).
Al igual que en la regresión lineal del capítulo 3, el algoritmo de aprendizaje debe atravesar las posibles funciones compatibles con el modelo subyacente, llamado M. En la regresión lineal, el modelo fue parametrizado por w. La función y = M (w) se puede probar para medir su costo.
Al final, elegimos un valor de w con el menor costo. La única diferencia entre la regresión y la clasificación es que la salida ya no es un espectro continuo, sino una salida discreta de un conjunto de etiquetas de clase.
EJERCICIO 4.1 ¿Es una mejor idea tratar cada uno de los siguientes puntos como una tarea de regresión o clasificación:
(a) predicción de los precios de las acciones,
(b) decidir qué acciones debe comprar, vender o mantener,
(c) evaluar la calidad de un computadora en una escala de 1-10
RESPUESTA (a) regresión, (b) clasificación, (c) otros/either
Dado que los tipos de entrada / salida para la regresión son incluso más generales que el de la clasificación, nada le impide ejecutar un algoritmo de regresión lineal en una tarea de clasificación. De hecho, eso es exactamente lo que haremos en la sección 4.3. Antes de comenzar a implementar el código TensorFlow, es importante medir la fuerza de un clasificador. La siguiente sección cubre los enfoques más avanzados para medir el éxito de un clasificador.
4.2 Medición del rendimiento
Accuracy (Exactitud)
¿Recuerdas esos exámenes de opción múltiple en la escuela primaria o en la universidad? Los problemas de clasificación en el aprendizaje automático son muy similares. Dada una declaración, su trabajo es clasificarlo como una de las “respuestas” de opción múltiple dadas. Si solo tiene dos opciones, como en un examen verdadero o falso, entonces lo llamamos un clasificador binario. Si se tratara de un examen calificado en la escuela, la manera típica de medir su puntaje sería contar el número de respuestas correctas y dividirlo por el número total de preguntas.
El aprendizaje automático adopta esta misma estrategia de puntuación y la llama precisión. La exactitud es medido por la siguiente fórmula:
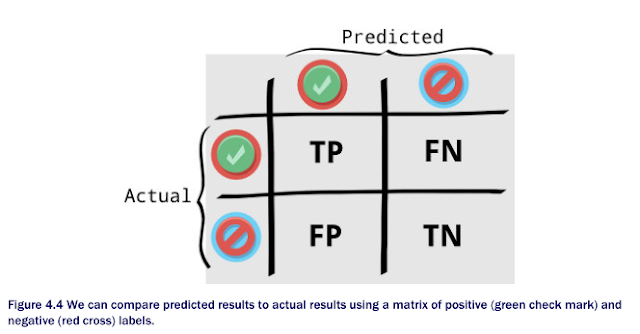
Esta fórmula ofrece un resumen aproximado del rendimiento, que puede ser suficiente si solo le preocupa la corrección general del algoritmo. Sin embargo, la medida de precisión no revela un desglose de los resultados correctos e incorrectos para cada etiqueta. Para tener en cuenta esta limitación, una matriz de confusión es un informe más detallado del éxito de un clasificador. Una manera útil de describir qué tan bien se desempeña un clasificador es inspeccionando cómo se desempeña en cada una de las clases. Por ejemplo, considere un clasificador binario con una etiqueta "positiva" y "negativa". Como se muestra en la figura 4.4, una matriz de confusión es una tabla que compara cómo se comparan las respuestas pronosticadas con las reales. Los elementos de datos que se pronostican correctamente como positivos se denominan verdaderos positivos (TP). Aquellos que se pronostican incorrectamente como positivos se llaman falsos positivos (FP). Si el algoritmo predice accidentalmente que un elemento es negativo cuando en realidad es positivo, llamamos a esta situación un falso negativo (FN). Por último, cuando la predicción y la realidad coinciden en que un elemento de datos es una etiqueta negativa, se llama un verdadero negativo (TN). Como podemos ver, se llama matriz de confusión porque hace que sea fácil ver con qué frecuencia un modelo confunde dos clases que intenta diferenciar.
Precisión y memoria (Precision and Recall)
Aunque las definiciones de verdaderos positivos (TP), falsos positivos (FP), verdaderos negativos (TN) y falsos negativos (FN) son útiles de manera individual, el verdadero poder está en la interacción entre ellos.
La relación de los positivos verdaderos al total de ejemplos positivos se llama precisión. Es una puntuación de la probabilidad de que una predicción positiva sea correcta. La columna de la izquierda en la figura 4.4 es el número total de predicciones positivas (TP + FP), por lo que la ecuación de precisión es la siguiente:
La relación de los positivos verdaderos a todos los positivos posibles se denomina "recall". Mide la relación de verdaderos positivos encontrados. En otras palabras, es una puntuación de cuántos verdaderos positivos fueron exitosamente predecidos (es decir, "recalled"). La fila superior en la figura 4.4 es el número total de todos los positivos (TP + FN), por lo que la ecuación para recordar es la siguiente:
En pocas palabras, la precisión es la proporción de tus predicciones que obtuviste, y recordar es la proporción de las cosas correctas que identificaste en el conjunto final.
Hagamos un ejemplo rápido. Digamos que estamos tratando de identificar a los gatos en un conjunto de 100 imágenes. 40 de las fotos son gatos, y 60 son perros. Cuando corrimos nuestro clasificador, 10 de los gatos fueron identificados como perros, y 20 de los perros fueron identificados como gatos. Nuestra matriz de confusión parece la siguiente matrix de confusión:
Puede ver el número total de gatos en el lado izquierdo: 30 identificados correctamente y 10 no,
totalizando 40.
EXERCISE 4.X
What’s the precision and recall for cats? What’s the accuracy of the system?
ANSWER
- For cats, our precision is 30/(30+20) or 3/5.
- The recall is 30/(30+10), or 3/4. The accuracy is (30+40)/100, or 70%
Curva característica de funcionamiento del receptor (Receiver operating characteristic curve)
Debido a que los clasificadores binarios están entre las herramientas más populares, existen muchas técnicas maduras para medir su rendimiento, como la curva de características operativas del receptor (ROC).
La curva ROC es un gráfico de compensaciones entre falsos positivos y verdaderos positivos.
El eje x es la medida de los valores falsos positivos, y el eje y es la medida de los valores positivos verdaderos. Un clasificador binario reduce su vector de entidad de entrada en un número y luego decide la clase en función de si el número es mayor o menor que un umbral especificado. Cuando ajustamos un umbral del clasificador de aprendizaje automático, trazamos los distintos valores de falso positivo y tasas verdaderas y positivas.
Una forma robusta de comparar varios clasificadores es comparando sus curvas ROC. Cuando dos curvas no se intersecan, entonces un método es ciertamente mejor que el otro. Los buenos algoritmos están muy por encima de la línea de base. Una forma cuantitativa de comparar clasificadores es midiendo el área bajo la curva ROS. Si un modelo tiene un valor de área bajo la curva (AUC) superior a 0.9, es un excelente clasificador.
Un modelo que adivina aleatoriamente la salida tendrá un valor AUC de alrededor de 0.5. Vea la figura 4.5 para un ejemplo.
EJERCICIO 4.2 ¿Cómo se vería como un punto en una tasa correcta del 100% (todos los verdaderos positivos, no los falsos positivos)? como un punto en una curva ROC ?
RESPUESTA
El punto para una tasa correcta del 100% se ubicaría en el eje y positivo de la curva ROC.









Comentarios
Publicar un comentario